Букмекер с многолетним опытом в организации азартных развлечений. Здесь каждый пользователь может найти развлечение по своему вкусу. Для любителей спорта на сайте представлено множество позиций спортивных мероприятий. Ценители азартных развлечений смогут по-истине оценить не только изобилие слотов, карточных и настольных игр, но также получат доступ к ТВ играм и live казино. Любители компьютерных игр смогут не только следить за важными события киберспорта на сайте Parik-24, но и улучшить свое финансовое положение, просто сделав ставку на любимую команду. Кроме возможности сделать ставку на спорт букмекер предоставляет функции просмотра событий онлайн. Это позволяет рассчитать коэффициент и совершить ставку достаточно быстро, не отрываясь от анализа турнира или спортивной игры.
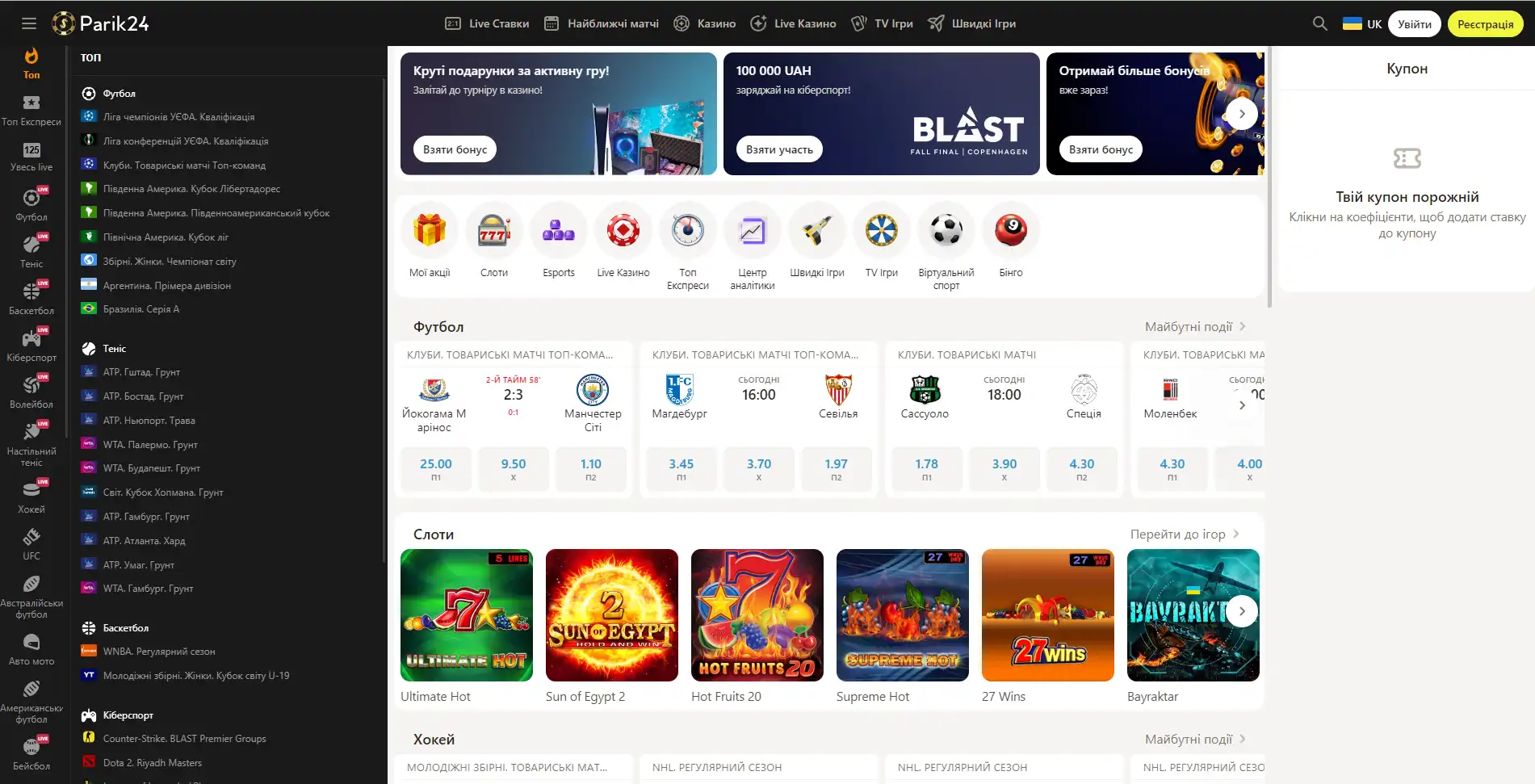
Парик 24 является не просто букмекерской конторой, проект принимает активное участие в развитии спорта и киберспорта, благодаря тому, что является спонсором многих соревнований.
Площадка позволяет протестировать свой игровой ассортимент, чтобы это сделать, нужно перейти в раздел "быстрые игры" и выбрать игру по вкусу. При клике на выбранный слот нужно выбрать кнопку "демо".
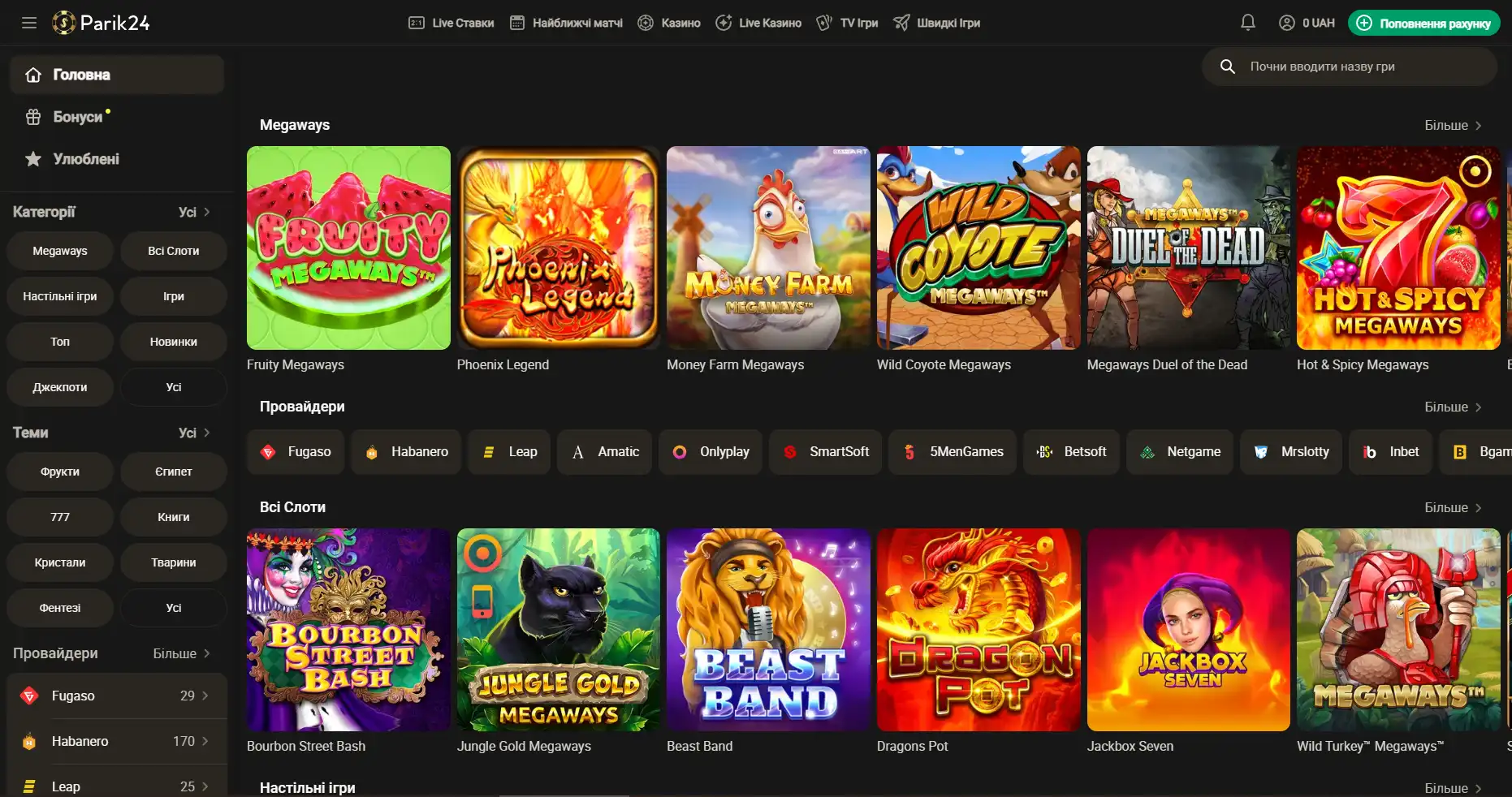
Регистрация на Парик-24
Чтобы взять по-максимуму от возможностей портала, необходимо пройти короткую регистрацию и верификацию. Это открывает перед пользователем отличные перспективы. Кроме того, что игрок сможет пополнять счет и выводить деньги, также будет возможность участвовать в различных турнирах с крупными джекпотами. На сегодняшний день есть два метода регистрации: с помощью телефона и электронной почты. Для начала необходимо зайти на официальный сайт и нажать кнопку "регистрация". Разберем детально, что они из себя представляют:
Регистрация с помощью мобильного телефона
- Выберите код страны.
- Введите номер телефона.
- Придумайте пароль.
- Отметьте валюту в которой предпочтете играть.
- Поставьте галочку, если вам более 18 лет.
- Нажмите кнопку "зарегистрироваться" для подтверждения создания аккаунта.
Регистрация с помощью e-mail
- Заполните строку для электронной почты.
- Придумайте надежный пароль.
- Выберите валюту для игр.
- Отметьте, если вам есть 18 лет.
Также каждый пользователь имеет возможность создать аккаунт используя свой профиль в Google. Для этого, в открывшемся окне, нужно выбрать "регистрация через Google", после чего процесс завершится автоматически.
Личный кабинет в БК Парик24
Личный аккаунт на сайте дает пользователю доступ к полному функционалу. Кроме возможности делать ставки на спорт и кибер спорт, играть в различные игры, это также возможность пополнять счет, выводить деньги и многое другое:
- Персональные данные. Здесь можно внести информацию о себе и изменить некоторые данные. Многие строки обязательны к заполнению. Важно, чтобы данные были внесены корректно, относительно документа, так как недостоверная информация может воспрепятствовать прохождению верификации.
- Подтверждение аккаунта. В этой категории нужно загрузить данные и фото выбранного документа.
- Мои акции. Раздел отображает доступные бонусы, активные поощрения, а также список уже использованных преференций.
- Баланс. Категория показывает остаток средств на счету, а также статистику пополнений и выводов денег.
- Ставки. Хранит данные о совершенных и активных на данный момент ставках.
- Настройки. Здесь доступна возможность настроить интерфейс сайта согласно своих потребностей. Выбрать язык, изменить пароль, выключить и выключить определенные уведомления. Также можно настроить уведомления касаемо ставок на спорт.
- Помощь. В данном разделе пользователь имеет возможность связаться со службой поддержки, а также перечитать правила площадки.
Бонусы беттинг-компании Parik-24
Портал дарит пользователям массу призов и бонусов. Неважно как давно вы зарегистрированы на сайте, поощрения получает как новичок, так и опытный игрок букмекерской конторы. На данный момент на портале активны следующие предложения:
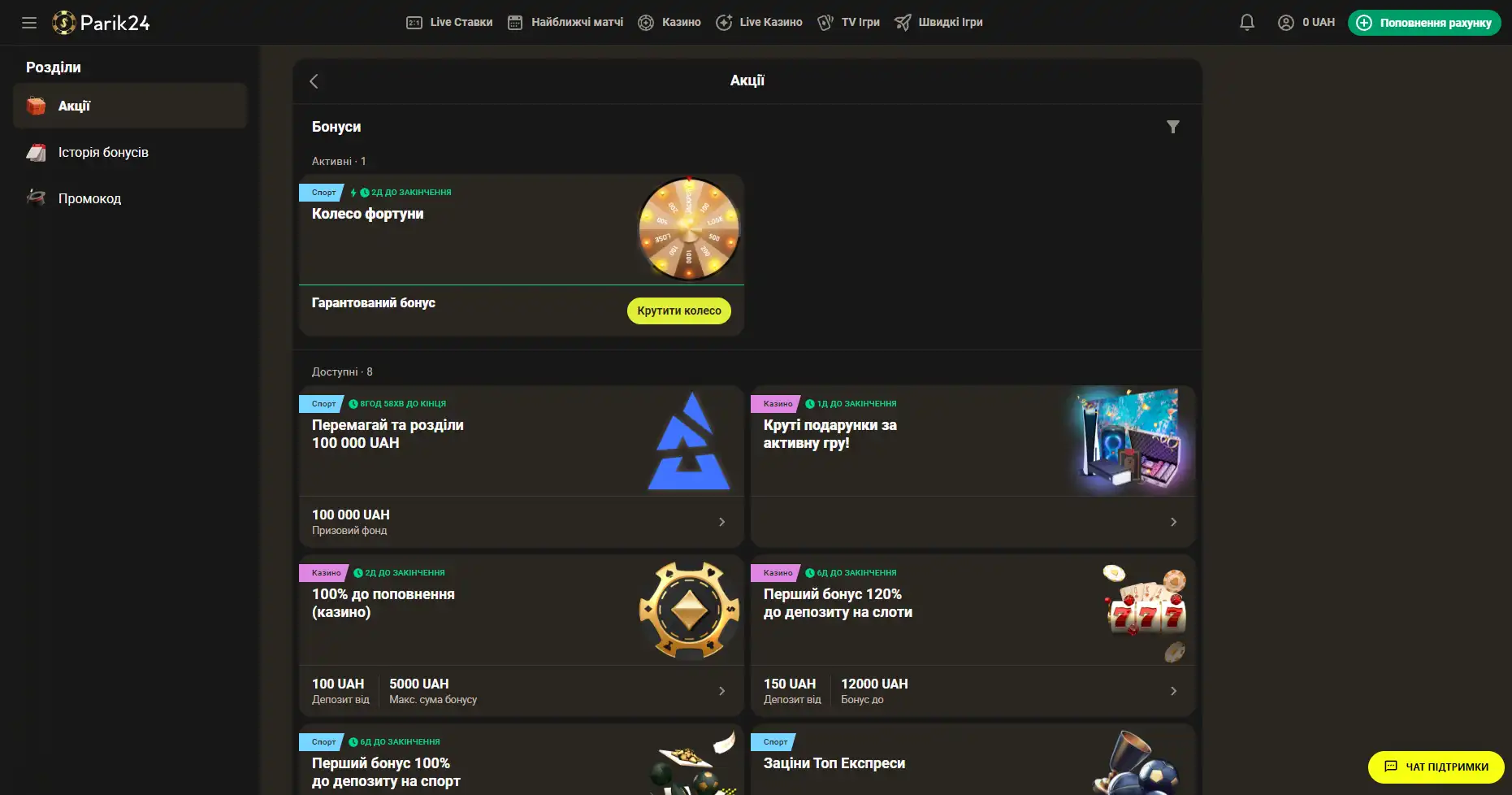
- Фрибет 300 гривен. Получить этот бонус можно совершая ставки на сумму от 4 тысяч гривен, два дня подряд. Фрибет означает возможность сделать бонусные ставки на сумму 300 гривен. Предложение действует в рамках квеста, который можно пройти дважды. При вторичном прохождении бонус увеличивается.
- Бонус к депозиту. При первичном пополнении счета, на сумму от 500 гривен, пользователь получает бонус в размере 100% к сумме пополнения, 100 фриспинов в игре Sun of Egypt 2, а также фрибет 200 гривен на любое спортивное мероприятие.
- Бонус активному игроку. На протяжении недели необходимо активно играть накапливая бонусы. В итоге самые активные игроки получат бонусные деньги в размере до 300 тысяч гривен.
- +100% к первому депозиту. Чтобы получить данное поощрение нужно пополнить счет на сумму от 150 гривен. Однако стоит заметить, что данный бонус необходимо отыграть.
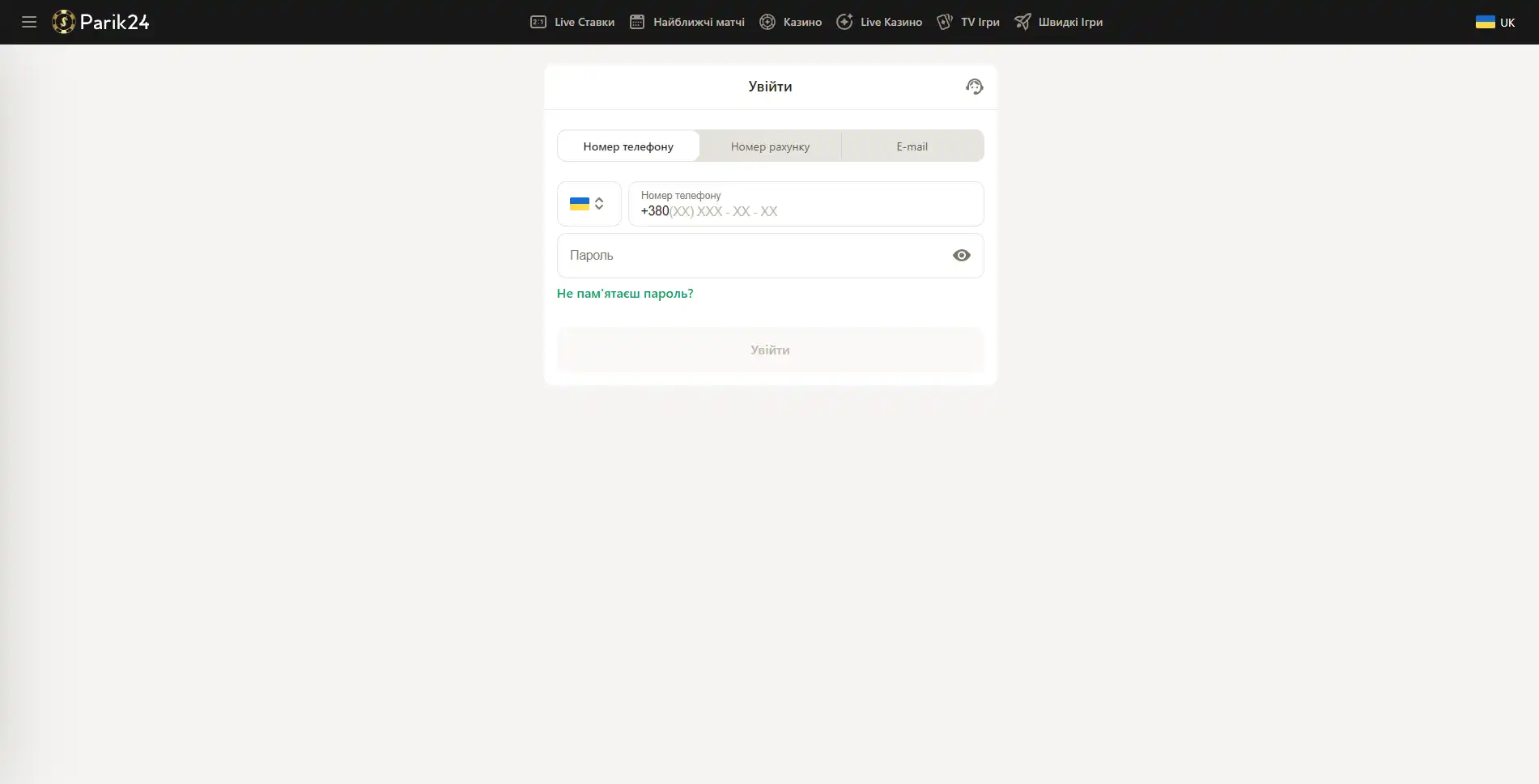
Вход в букмекерскую контору Parik-24
Чтобы испытать свою удачу в азартных играх или аналитические способности в ставках на спорт, нужно зайти на сайт и авторизоваться в личном кабинете.
Возможные проблемы со входом
Порой пользователи сталкиваются с проблемой доступа на сайт. Это обусловлено тем, что портал блокируется со стороны провайдера. Также, как вариант это может быть техническое обслуживание портала специалистами. Существует несколько способов, чтобы не смотря ни на что попасть в личный кабинет:
Зеркала сайта - они представляют собой дополнительные сайты, которые находятся по другому адресу. Владеть свежими данным относительно рабочих зеркал поможет подписка на социальные сети букмекерской конторы. Также, в качестве альтернативного варианта, можно использовать обращение в поддержку. Менеджеры беттинг-компании работают круглосуточно.
TOR - его можно назвать браузером, только он имеет дополнительные функции, которые обеспечивают обход любой блокировки.
VPN службы - это специальное программное обеспечение, скачать его можно как на телефон, так и на компьютер. Он позволяет получить беспрепятственный доступ к заблокированным сайтам, благодаря тому, что меняет ваш ip адрес на другой.
Прежде чем воспользоваться сторонними программами, стоит внимательно ознакомиться с правилами установки и использования. Также, администрация Парик24 рекомендует использовать для загрузки только проверенные источники.
Портал доступен для использования на любом устройстве. Мы рассмотрим авторизацию с каждого из них.
Вход с помощью компьютерной версии Parik-24
Версия сайта для компьютера позволяет оценить уровень графики и анимации в играх. Трансляции спортивных мероприятий также гораздо удобнее смотреть на компьютере. Чтобы войти в личный кабинет, нужно посетить главную страницу портала и нажать кнопку "войти" и после этого в новом окне ввести следующие данные:
- Внести номер телефона, номер счета или электронную почту.
- Заполните строку для пароля.
- Проверьте введенную информацию.
- Нажмите кнопку "войти".
В качестве альтернативного варианта для входа можно использовать свой профиль в Google. Для этого нужно нажать ссылку "вход через Google" и выбрать ваш аккаунт в данном сервисе.
Вход через мобильное приложение
К сожалению приложение Парик-24 еще находится в разработке, в скором времени оно будет доступно на всех устройствах. Но пока рекомендуем воспользоваться мобильной версией сайта. Такой формат имеет свои преимущества - например отсутствие необходимости в скачивании дополнительных файлов.
Вход с помощью мобильной версии
Портал букмекерской конторы разработан в адаптивном формате. Это позволяет получить качественный контент и обширный функционал на любом устройстве. Мобильная версия не требует дополнительных скачиваний игр, благодаря тому, что развлечения разработаны на HTML5, они не занимают дополнительной памяти на вашем телефоне. Пользуясь сайтом с помощью других устройств, вы не ощутите существенной разницы в интерфейсе и функциях. Для авторизации в личном кабинете зайдите на главную страницу и воспользуйтесь кнопкой "войти", после чего следуйте инструкции ниже:
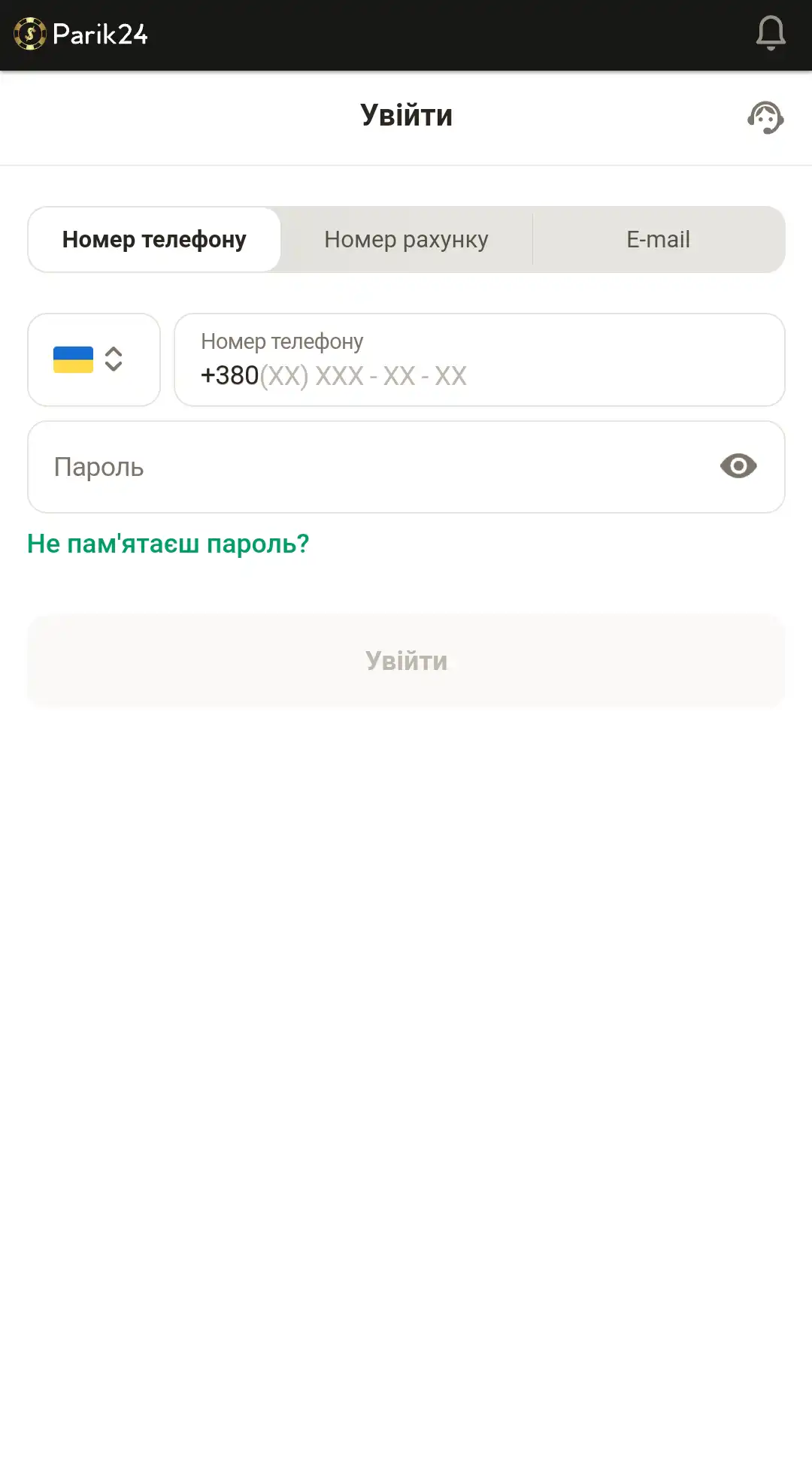
- Введите номер телефона, номер счета или электронную почту.
- Внесите пароль.
- Проверьте, верная ли информация.
- Кликните кнопку "войти", чтобы завершить процедуру авторизации.
- Или используйте пометку "войти через Google", если хотите использовать свой профиль данного сервиса.
Верификация
Верификация - это проверка личности пользователя. Она нужна для того, чтобы проверить возраст игрока и его данные. Дело в том, что по закону азартные развлечения запрещены для несовершеннолетних пользователей. Чтобы пройти поверку нужно зайти в личный кабинет и выбрать раздел "Подтверждение аккаунта". Далее стоит выбрать документ, с помощью которого вам было бы удобнее пройти верификацию: паспорт, водительское удостоверение, заграничный паспорт. После этого ознакомьтесь с правилами по созданию фото документа, сфотографируйте его и загрузите специальной кнопкой "Загрузить из галереи". Обычно проверка проходит в течении нескольких дней. Убедитесь, что в разделе "Персональные данные" вы ввели достоверную информацию, в противном случае это может отразиться на результате проверки.
Не стоит волноваться за сохранность личной информации. Все данные на сайте букмекера Парик-24 проходят шифрование и хранятся на защищенных серверах беттинг-компании.